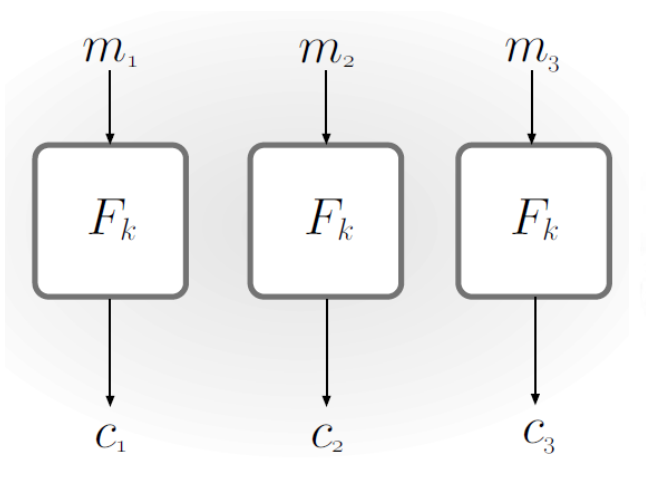
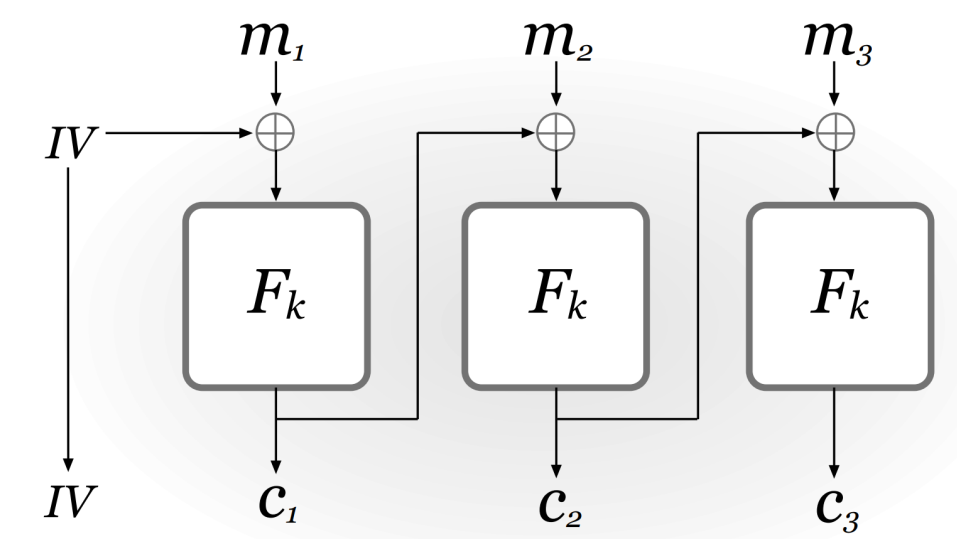
密码学与信息安全基础-CS3314

计算机安全概况
密码理论与技术
- 经典加密技术
- 常用密码算法
- 保密通信技术
- 公钥密码算法
- 消息认证和Hash函数
- 认证协议
网络安全实践
- 认证服务
- IP/Web安全
- 安全邮件
  Lec1 序论-计算机安全概况

安全定义

安全性(security)是一种抵御可能的风险和威胁的能力，而我们只关心由于人为因素所产生的风险和威胁。
威胁（threats）是对安全的潜在破坏。这种破坏不一定要实际发生才成为威胁。
攻击(attack)是可能导致破坏的行为，行为人被称为攻击者。
信息安全涉及到信息的保密性(confidentiality)、完整性
(integrity)、认证性（数据来源的可靠性） (Authenticity)、不可否认性(Non-repudiation)、可控性(controllability)
安全性是绝对的，还是和其它因素相关联的？

安全防护

安全服务安全策略与安全机制

提供安全服务（securityrelated services）
- 使得系统安全得到保护而免受威胁
制定安全策略（security policy）
- 安全策略能辨识威胁，并定义出能够确保系统安全的条件 (是对允许什么、禁止什么的规定)
- * 策略可以是==非技术的==，如在改口令前要求身份认证；策略常需要技术无法实施的过程性操作。
完善安全机制（security mechanisms）
- 负责检测和预防攻击，以及从攻击中成功地恢复工作(实施安全策略的一种方法、工具或者规程 )

安全模型

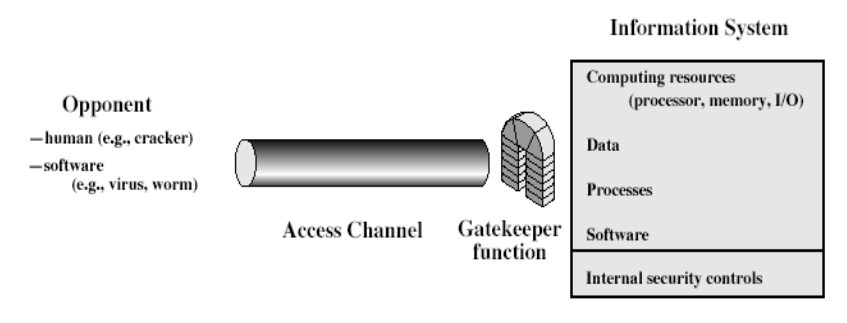
网络安全模型
访问控制安全模型

密码学理论与技术

Lec2 古典加密技术

密码系统的组成
- 五元组，对称与非对称密码
- 密码分析中的统计方法
- 主要的密码攻击类型
古典密码方法
- 代换密码
- 置换密码
  密码学基本概念
密码系统的完备性基础
$\begin{aligned} C = E(P, K_1) \\ P = D(C, K_2) \end{aligned}$
C（CyperText 密文） P（Plaintext 原文）

密码系统的构成
密码系统是一个五元组$(M, C, K, E( ) , D( ) )$ 满足下列条件：
- M是可能明文的有限集（明文空间）
- C是可能密文的有限集（密文空间）
- K是一切可能密钥构成的有限集（密钥空间）
密码分析：穷举/强力/分析（以下为分析法）
- 唯密文攻击
  - 从已知的密文中恢复出明文或密钥；
- 已知明文攻击
  - 从已知密文和一些明文-密文对中分析明文；
- 选择明文攻击
  - 可选定任意明文-密文对进行攻击；
- 选择密文攻击
  - 分析者能选择不同的被加密的密文，并能得到对应的解密的明文（主要用于公钥算法）
- Kerckhoff假设
  - 一个密码系统的安全性都应该基于密钥的安全性，而不是基于算法的细节的安全性
  - 原因
    - 容易保存
    - 容易分享
    - 防止反向工程
    - 容易更换
  - 结论：公开的密码学设计
    - 更多的实践检验
    - 更容易发现漏洞
    - 避免反向工程的危害
    - 利于构建标准
信息论基础
- 信息就是排除不确定性
- 概率越小的事件，信息量越大
密码体制的分类
- 单钥体制（对称密码体制） $K_1 = K_2$
  - 系统的保密性大于密钥的保密性。
  - 高速加解密
- 双钥体制（公钥密码体制） $K_1 \neq K_2$
  - eg. 流密码
  - 易更换
无条件安全（完善保密 unconditional secure）
- 无论有多少可以使用的密文，都不足以唯一确定由该体制善生密文所对应的明文。
- 在惟密文攻击条件下，如果一个密码系统其密文和铭文之间的相互信息为0，即 $I(M;C) = 0$，则该系统为完善保密的。
  - 其必要条件为$H(K) \ge H(M)$
计算安全（computational secure）
- 破译密码的代价超过了密文信息的价值
- 破译密码的时间超出了密文信息的有效生命周期

古典密码技术

代换(Substitution)
- 明文字母替换为其它字母、数字和符号
换位/置换(Transposition)
- 对明文字母的某种置换取得一种类型完全不同的映射

基于代换技术的古典密码体制

Caesar

移位代换
穷举可解
- 算法已知
- 密钥空间仅25个元素（25种偏移量）
- 明文可读

-> 移位密码

=> ==安全密码体制的密钥空间必须足够大==

单表代换密码

对于密钥穷搜索无效
但由于语言的统计特性，依然不安全
- 字母的使用频率是不同的
- 字母组合的使用频率也是不同的

-> 仿射密码

特殊情形的代换密码
- $E(x) = ax + b(mod 26), a,b \in Z_{26}$
- 密钥空间 12*26
解密
- 乘法逆元
  - $x=a^{-1}(y-b)(\mod m)$
单表代换的弱点:
明文的统计特性（语法和明文结构）原样地传递给了密文中!

多表代换密码

Playfair

将明文中双字母音节作为一个单元，并将其转换为密文的双字母音节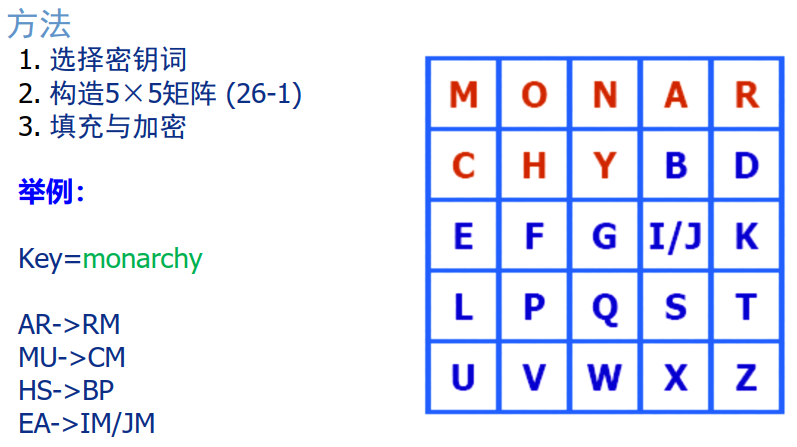

加密规则
- 预处理明文: 两个字母一组；若两个字母一样，则填充某个固定字母，重分组；
- 如： Balloon —》 ba lx lo on
  - 一组中的两字母同行，则每个字母用该行的后一字母替代；
  - 一组中的两字母同列，则每个字母用该列的后一字母替代；
  - 非同行同列字母替代，用对角的两个字母替代
分析
- 26× 26种双字母组合，对单字母判断困难
- 频率分析变得困难：双字母频率统计规律弱于单字母

Hill

一次加密多个字符，多表代换
m个连续明文字母被m个密文字母代替。由m个线性方程决定替代方法。

使用矩阵的逆进行解密即可。

优点：完全掩盖单字母频率特性（双字母，三字母。。。）。
可以抵抗已知密文攻击
缺点：不能抵抗已知明文攻击
- 当K为m×m矩阵，则获取m条（明文，密文）对，就可能获得密钥

Vigenère Cipher

使用多个单字母替换表, 因此一个字母可以被多个字母替换;
密钥的每一个字符确定加解密使用哪个字母表；
密钥的第i个字母表示使用第i个字母表；
依次使用每个字母表；
密钥周期使用。

（每隔r的整数倍，出现单表代换。）

密码分析：Kasiski方法
- 猜测r的可能值（利用密文中重复字符间距的最大公约数）
- 测试r是否为密钥长度
  - 分割子序列并计算重合指数（是否接近0.065）

一次一密 OneTimePad

来源于Vernam密码，基于二进制数据
- 密钥管理困难
- 安全性来自随机性
- 不可破译
密钥长度至少和待加密明文一样长
可扩展（可篡改）

基于置换技术的古典密码体制

置换密码
- 打乱明文字母的顺序
栅栏加密
- 密文以对角线顺序写为几行，并按顺序读出来。
换位技术
- 明文携程矩阵块，再按列读出，但是打乱列顺序

-》对简单的换位：将密文直接写为矩阵块，再推证列的次序

乘积密码

连续使用几种密码来增加破译的困难性
转轮机 Roter Machine
- 原理：非常复杂多变的代换密码（无perm）
- 方式：使用一系列的圆筒（每个圆筒是一个多表替换），每个圆筒相当于给出一个周期为26的多表代换算法

隐写术

严格来说，并不是加密
隐藏消息的存在
- 使用长消息作为代价来隐藏少量的信息
eg. IoT-SmartConfig
- 利用wifi中的802.11协议信息的长度分段来传递信息

结论

本章涉及的全部密码体制除OTP以外都是不安全的
此处的“安全”指：唯密文攻击/计算安全
- OTP在唯密文攻击下无条件安全
  2TP是不安全的
以Ad-Hoc的方式，或者以“简单方法”，不可能设计出安全的密码体制
- Simple and dirty的体制是不可行的
充足密钥空间准则：
- 密钥空间的大小必须足以防止穷搜索攻击。这是一个必要而非充分条件
设计安全的密码是一个困难的工作

Lec3-4 常用密码算法

分组密码相关概念
Feistel类密码
DES算法的主要构成
- 对DES的主要评价
分组密码的设计准则与应用模式
三重DES（构造、特点）
IDEA算法（构造、特点）
AES算法（构造、特点）
SM4算法（构造、特点）

对称加密

流密码

按位/字节连续、顺序地处理

首先产生一个密钥流，常常采用逐比特/字节异或
Vigenere, Vernam密码

和OTP的安全性比较？

OTP：P.S. K密钥>=P明文
Steam Cipher：C.S. K密钥\<P明文

分组密码

对明文信息分组/块、按组逐一处理

可以看作极大长度字符（64bit或更多）的代换
理想分组密码
- 均匀随机选取所有可逆变换
- 对于单个分组，可以达到理想的安全性
- 不具有可压缩性

SPN密码

Substitution Permutation Network 代换-置换网络

Shannon
S盒子+P盒子
目的：
- 混淆
  - 使得密钥和密文的统计关系尽可能复杂
- 扩散
  - 使得明文的统计特征消散在密文中

初步做法：CDP

Confusion Diffusion Paradigm

S-box和P-box即密钥k

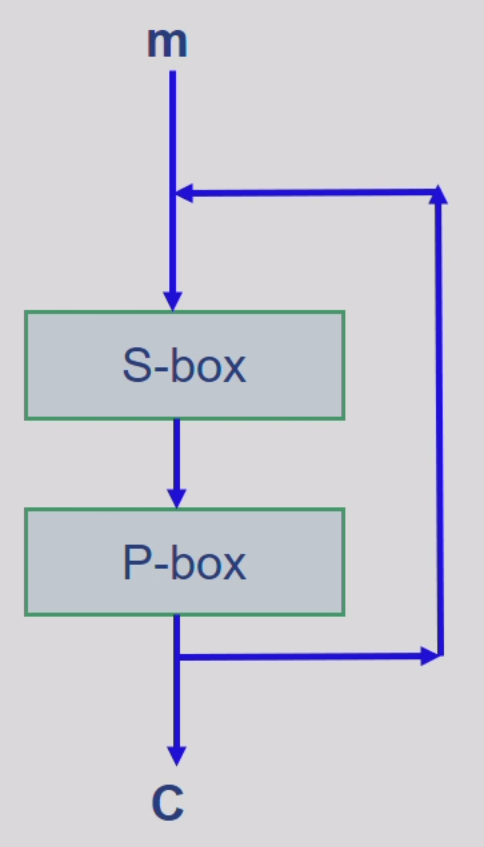
进一步的做法：SPN

公开/固定S-box和P-box
取而代之使用密钥策略，主密钥推出轮密钥

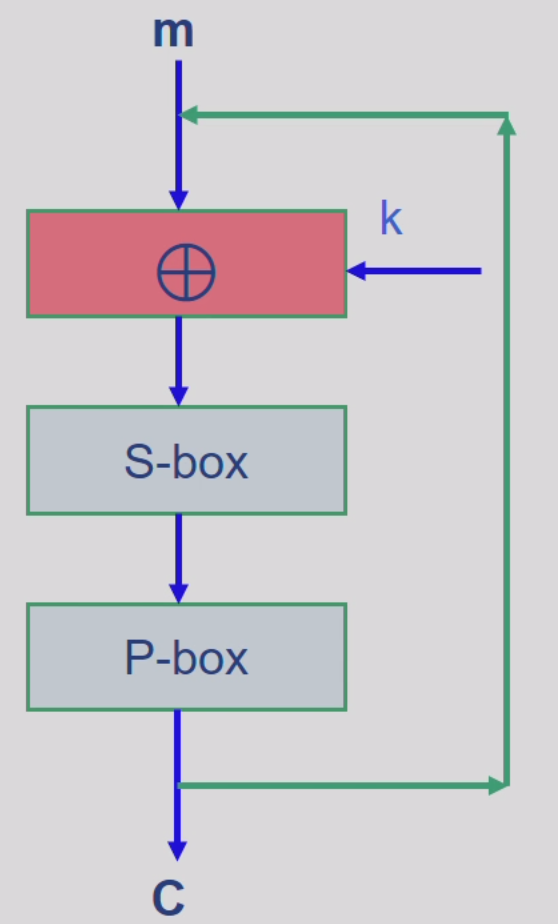
Feistel密码

使用基于可逆的乘积密码的思想来逼近简单代换函数
一种特殊的SPN
- 每组分为两半，执行多轮迭代
- 代换作用于左半，代换后左右两半进行置换

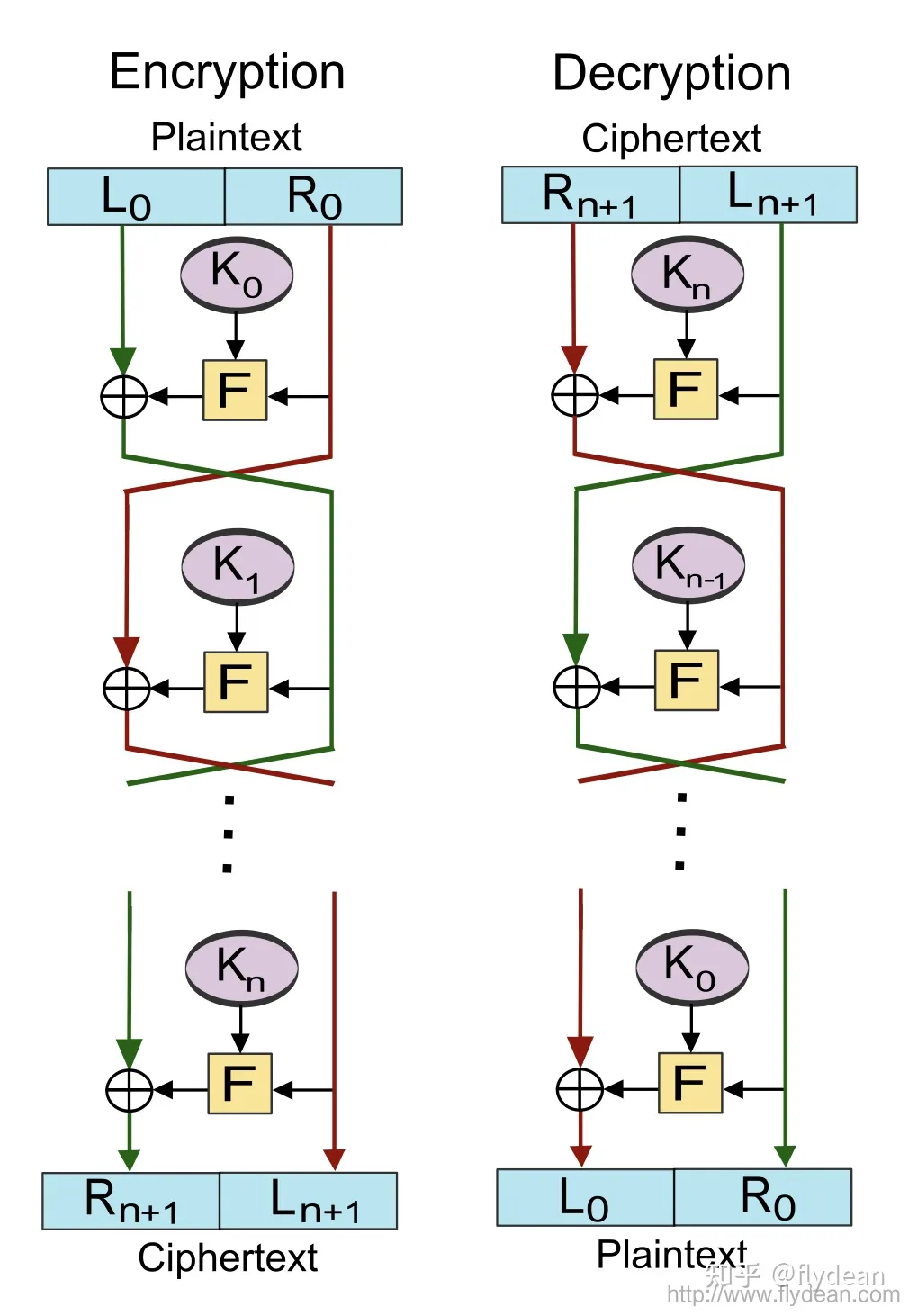
DES算法

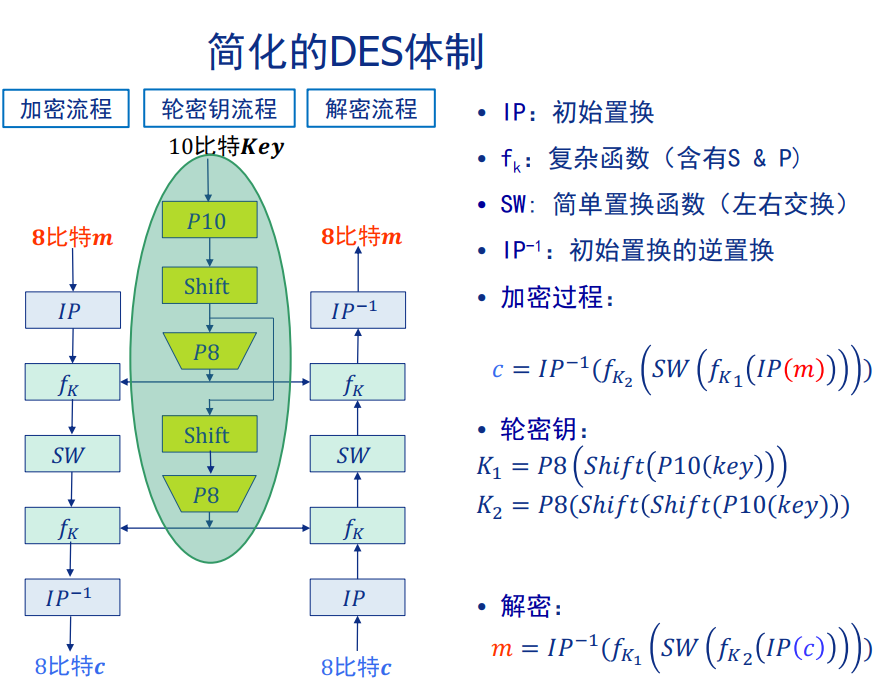
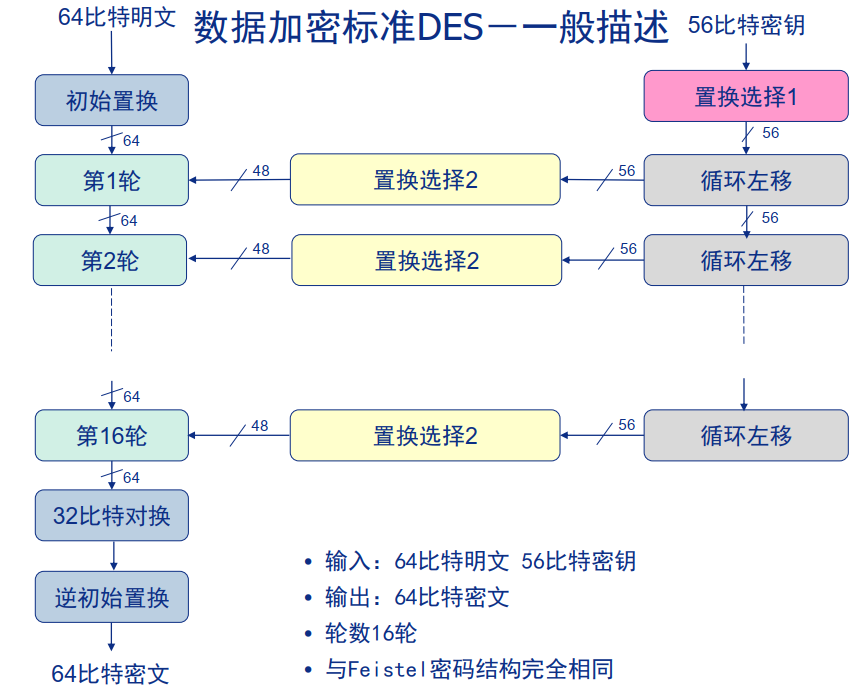
DES的单轮变换

分组长度：64bit
密钥长度：56bit，实际上密钥为64bit，不过有8bit为奇偶校验位
子密钥长度：48bit
扩展置换：32bit到48bit
S盒：有8个S盒，每个S盒进6bit出4bit。每个S盒对应一个4*16的矩阵，进入S盒的2bit决定行，4bit决定列，行列决定的那个元素就是S盒的输出
轮函数$F$：消息$R(32bit)$作为第一个输入，子密钥$K(48bit)$作为第二个输入，产生长度为32bit
- 对第一个参数$R$，利用扩展函数扩展成48bit的$E(R)$
- 计算$E(R) \bigoplus K$，结果记作8个6bit $B=b_1b_2b_3b_4b_5b_6$
- 使用8个S-box，$S_1S_2…S_8$，每个S盒可以看作是一个固定的4*16矩阵
- $b_1b_6$决定行数$r$，$b_2b_3b_4b_5$决定列数$c$
- 最后$P$为固定置换
密钥编排算法：
- $PC-1$：56bit置换
- $LS1$：移位操作，移多少位由轮数决定。比如，第1、2、9、16轮移动1bit，其余移动2bit
- $PC-2$：压缩置换，56bit到48bit。将前28bit中的24bit置换，并去掉9、18、22、25位；将后28bit中的24bit置换，并去掉35、38、43、54位
- 可以列出16张表对应16轮中使用的密钥，表中的元素表示48bit的子密钥使用了56bit密钥中的哪些位

DES的核心是S-box，除此之外的计算是线性的。
在实际使用中，可以采用双重DES与三重DES。其中，

双重$DES$：在加密之后，再用另一个密钥进行加密。但它易受中间者攻击，与DES的安全性无明显区别。
三重$DES$：先用一个密钥加密，再用另一个密钥解密，然后再用第一个密钥加密$C=E{k1}(D{k2}(E_{k1}(P)))$，解密时使用对应密钥解密即可，密钥长度达到112bit（可以防范中间者攻击）

IDEA

可以对抗差分密码攻击，非S-P盒类型

分组长度64bit，密钥长度128bit，同一算法既可加密又可解密
IDEA的“混淆”和“扩散”设计原则来自三种运算：
- 逐位异或
- 模$2^{16}$的整数加
- 模$2^{16}+1$的整数乘
子密钥16bit
子密钥编排算法：52个16bit的子密钥从128bit的密钥中生成
- 前8个子密钥直接从密钥中取出
- 对密钥进行25bit的循环左移，接下来的密钥就从中取出

IDEA的解密：

加解密实质上没有区别，但使用不同的密钥
解密密钥从加密密钥中导出

AES

Rijindael的轮函数每一轮迭代的结构都一样，由下述4个不同的变换构成，只是最后一轮省略了列混合变换

字节替换：对数据的每一字节应用一个非线性变换——应用一个替代表，表中纵向的x取自状态矩阵中高4bit，横向的y取自低4bit
行移位：对每一行的字节循环重新排序
列混合：对矩阵的列应用一个线性变换——将状态的每一列视为$GF(2^8)$上的多项式$S(x)$，然后乘以固定多项式$a(x)$，并$mod \; x^4+1$
轮密钥加：把轮密钥混合到中间数据——对状态和每轮的子密钥进行简单的异或操作

当密钥长度分别为：128、192、256bit时，分别要加密10、12、14轮，且第一次轮密钥加也要用到一轮子密钥。比如，对于AES-128来说，共需要$128 \times 11=1408bit$ 的密钥

子密钥生成：

SM4

Lec5 分组码应用模式与伪随机数

分组密码常见工作模式及各自优缺点
- 电码本模式
- 密文分组链接模式
- 输出反馈模式
- 密文反馈模式
- 计数器模式
伪随机数
- 与真随机数的区别
- 评价标准
- 典型生成方式
  ECB (Electronic CodeBook)
弱点：对各个明文组的加密相互独立
多个数据组缺乏安全性（可交换）

CBC (Cipher Block Chaining)

消息分块后通过加密进行连接
- 将上一密文组与新的铭文组异或后再进行加密和链接
适用于大量数据的加密和认证
- 即使只有一个Block不同也会使得后继Block的加密结果完全不同
最后一个消息分组如小于64Bit，需要填充
- 方法一：NULL
- 方法二：写入填充个数
需要初始向量IV
- 不可以通过历史信息推测出下一个初始向量
- 必须随机选择！
如果攻击者获得了IV，可通过预先改变IV的一些位使得接收者的明文中部分位被取反
- 解决方法：在发送消息前用ECB保护IV
解密：
- 对每个块分别解密并与上一个块的密文进行异或，可以并行解密
  CFB (Cipher FeedBack)*

OFB (Output FeedBack)

加密函数的输出被反馈回到移位寄存器作为下一次的输入而非密文单元
密钥流可以提前运算，但是该类型密钥流（FB密钥流）不能够并行计算。

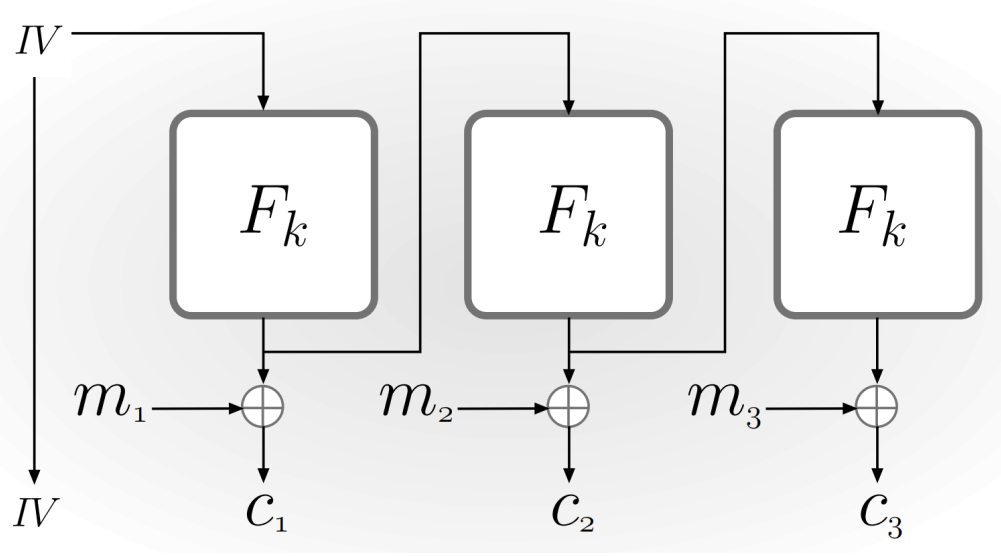
优点
- 传输过程中，比特差错不会扩散
- 可以预计算分组，流加密时不需停顿
缺点
- 对抗消息流篡改攻击的能力弱于CFB：若对密文取反，则解密后的明文也取反
- 可以看作是一次一密的变形（Vernam密码）
  - 所以绝对不能重复使用相同的密钥序列和IV
- 发送方和接收方必须同步

CTR (Counter)

与OFB相似处：明文与分组的输出异或得到密文。
与OFB的差异：分组加密的输入是计数
对每个明文，必须使用不同的分组密钥和计算器值（绝不重用）

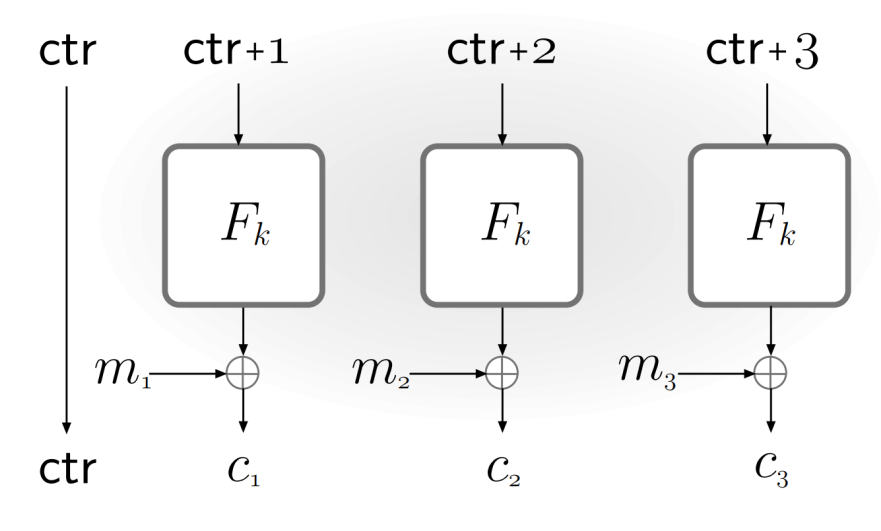
优点
- 高效
- 可以并行处理多块明文密文
- 可以预计算
- good for bursty high speed links
- 随机访问：密文的第i个分组可以随机访问，不需知道前面i-1个密文组（比较： CBC）
- 可证安全：是CPA安全的
  - 前提：使用了真正的随机数生成器，且每个计数器值绝不重用
缺点
- 密钥、计数器值绝不能重用

分组码应用模式小结

https://zhuanlan.zhihu.com/p/520658724

ECB电码本 -> Basic mode
除ECB以外的模式中，解密均需要初始值（IV/CTR）。初始值必须随机选择。

C** -> 在下一个明文块加密时使用上一个块的密文结果
CBC Block chaining 意为分组链接，不支持流加密
但是有一定程度的差错扩散。
五个模式中，仅CBC才用了先异或后加密的方式，其它均为先加密后异或。（即密文是明文经过一定处理后异或得到的结果）
CFB cypher feedback，把密文的移位作为了下一个块的加密参数，计算得到密钥后与明文异或。

*FB -> 每次加解密时加密函数使用了不同的参数值，这依赖于上一个块的某些步骤
CFB 新的块加密参数来源于上一个块的密文的移位
OFB 新的块加密参数依赖于上一个块的块加密参数的加密结果
加密均不能并行，不过OFB的密钥流可以提前分离计算。
均可以并行解密。

CTR 计数器
与OFB均产生密钥流。与OFB不同在于没有FB过程，块加密参数来源于计数器的自增。
因为计数器的增加是独立的，所以可以随机加解密、并行加解密。
使用密钥流的方法均不会有差错扩散。

模式名称	可流加密？	可并行加解密？	有差错扩散？
ECB（Electronic Codebook）	否	是	否
CBC（Cipher Block Chaining）	否	否（解密可并行）	是
CFB（Cipher Feedback）	是	否（解密可并行）	是
OFB（Output Feedback）	是	否	否（密钥流）
CTR (Counter)	是	是	否（密钥流）

随机数

随机数的用途
- 认证方案(nonce)
- 会话密钥的产生
- RSA公开密钥加密算法中密钥的产生
检验随机程度的两个准则
- 均匀分布：出现概率大致相等
- 独立性
不可预测性
- 可以证明， PRG的安全性与不可预测性是等价的

伪随机数产生器 (C++ 的RND)

线性同余法
- m 模数 m>0
- a 乘数 $0 \le a<m$
- c 增量 $0 \le c<m$
- $X_0$ 初始值 $0 \le X_0<m$
一般将m选为一个给定的计算机所能表示的最多非负整数
此方法受到很彻底的测验
攻击方法
- 若知道a, c, m，则由一个随机数可以知道后继随机数
- 即使只知道使用该算法，且知道了四个连续随机数，形成三个线性同余式，就可恢复a, c, m
- 结论：一旦知道序列的一小部分，不可预测程度就变得很差

用分组密码产生的随机数

BBS产生器 (Blum整数)

基于公钥算法，是现在广泛使用的安全随机数产生方法
选择两个大素数，满足 𝑝 ≡ 𝑞 ≡ 3 (mod 4)
- $𝑁 = 𝑝𝑞$
- 选择𝑠与𝑁互素
  - $X_0 = s^2 mod N$
- 输出：
  - $𝑋𝑖 = (𝑋{𝑖-1})^2 mod 𝑁$
  - $𝐵𝑖 = 𝑋𝑖 mod 2$
优点
- 在续位测试下，满足不可预测性：不存在多项式时间算法，在给定序列的前k位输入时，以不可忽略的概率预测出第k＋1位
- 安全性基于分解大整数N的困难性
- 给定任意已知bit仍满足不可预测性
缺点
- 很慢，因为𝑁必须很大
- 对密码学应用而言太慢了，仅适用于密钥生成

Lec6 保密通信

Lec7 消息认证和Hash函数（认证性）

消息认证的定义
三类认证函数各自的特点及作用
Hash函数的特点，及三大性质
MAC与对称加密的区别， MAC的使用方式
消息认证和认证函数

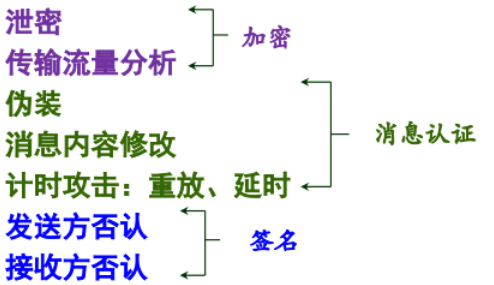
三类产生认证符的函数

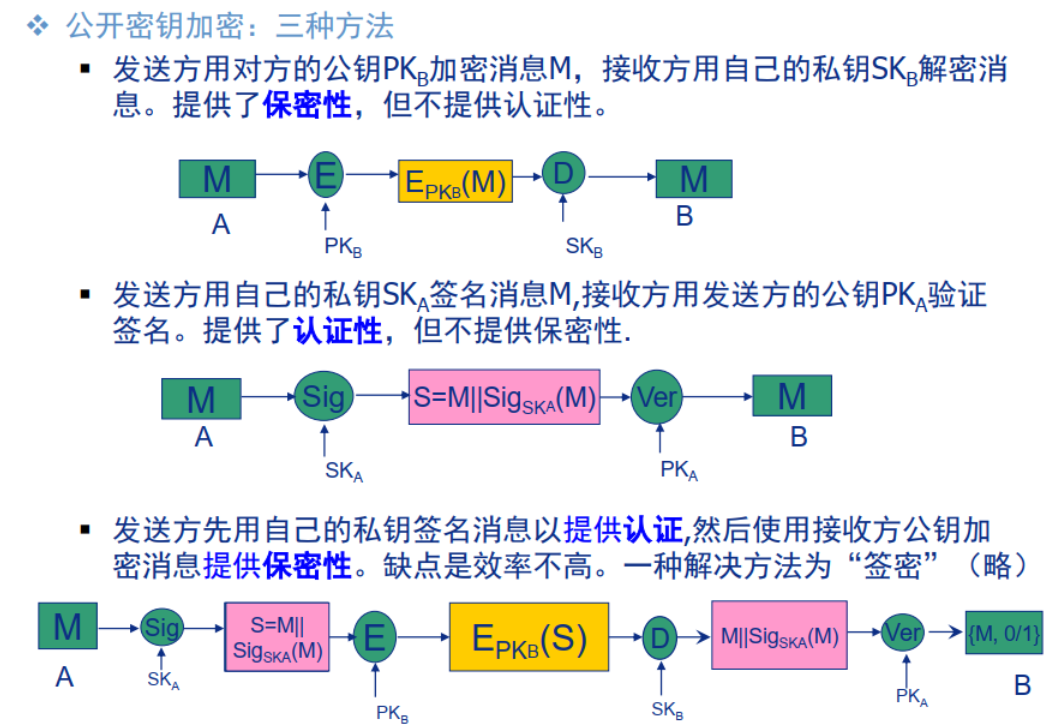
消息加密（常规加密，对称）：属于对称加密（仅A和B共享密钥K），提供保密和一定程度的认证，但不提供签名（发送者可以否认报文，接收者可以伪造报文）
消息加密（公钥密码，非对称）：发送方用接收方的公钥加密信息，接收方用私钥解密，该方案不提供认证；发送方也可以先用自己的密钥加密以提供认证，然后使用接收方公钥加密提供保密性，但这样效率不高

报文加密：以整个报文的密文为认证码

作用： 主要目标是保护报文的隐私和机密性，确保未经授权的用户无法理解报文内容。
过程： 将整个报文使用加密算法和密钥进行转换，生成密文。只有知道正确密钥的接收方才能解密并还原原始报文。
注意： 报文加密通常不直接提供完整性验证或身份认证。它专注于隐藏报文内容，而不涉及验证报文是否被篡改。

报文认证码（MAC）：以一个报文的公共函数和用于产生一个定长值的密钥作为认证符

作用： 用于验证报文的完整性和真实性，确保报文在传输过程中没有被篡改，并且是由合法发送方生成的。
过程： 使用一个密钥和某个报文认证码算法，对整个报文进行转换生成一个固定长度的认证码。接收方使用相同的密钥和算法来验证认证码。
注意： MAC结合了报文内容和密钥，因此只有知道密钥的人才能正确生成和验证认证码。

散列函数：一个将任意长度的报文映射为定长的散列值的公共函数，以散列值作为认证符

作用： 用于生成报文的摘要，通常用于完整性验证和防止篡改。散列函数将任意长度的输入映射为固定长度的输出。
过程： 报文经过散列函数处理，生成散列值，这个散列值可以看作是报文的“指纹”或“摘要”。
注意： 散列函数通常是公共函数，不需要密钥。虽然它不能提供身份认证，但在验证报文完整性方面很有用，因为即使报文发生微小变化，散列值也会显著改变。

综合使用这些机制可以构建更强大的安全系统。例如，常见的做法是将报文先进行加密以保护隐私，然后使用MAC或散列函数来验证完整性。

报文加密

对称加密

用户A为发信方，用户B为接收方。用户B接收到信息后，通过解密来判决信息是否来自A，信息是否是完整的，有无窜扰。
对称加密与认证的关系

A向B发送: $E_K (M)$

提供保密(仅A和B共享密钥K)
提供一定程度的认证
- 仅来自A
- 传输中不会被更改
- 需要某种结构或冗余，以识别合法明文
不提供签名
- 接收者可以伪造报文
- 发送者可以否认报文

公钥加密

散列函数

散列函数是将任意长度的消息映射成一个较短的定长输出消息的函数.
形式: h = H(M), M是变长的消息，h是定长的散列值.
散列函数的目的是为文件、报文或其它的分组数据产生数字指纹
不同的称呼
- 散列函数
- 杂凑函数
- 消息摘要函数
- 哈希(hash)函数
适用范围
- H能用于任何大小的数据分组;
- H产生定长输出;
数学性质
- 对任意给定的x, H(x)要相对易于计算,使得软硬件实现都实际可行;
- 单向性：对任意给定的码h, 寻求x使得H(x)=h在计算上是不可行的;
- 弱抗碰撞性：任意给定消息x, 寻求不等于x的y, 使得H(y)= H(x)在计算上不可行
- 强抗碰撞性：寻求对任何的(x,y)对使得H(x)=H(y)在计算上不可行
对输出长度为m的Hash函数，值$2^m/2$决定了该Hash函数抗穷举攻击的能力

散列函数的算法
简单散列算法
- 容易碰撞，但是可以用于模式匹配
安全散列算法
- MD系列
- SHA系列

MD5算法

步骤1：
添加填充位(一个1 和若干个0)。在消息的最后添加适当的填充位使得数据位的长度满足$length \times 448 (mod\, 512)$
步骤2：
添加长度。原始消息长度（二进制位的个数），用64位表示。如果长度超过264位，则仅取最低64位，即mod 264。到此为止，我们已经得到一个长度为512位的整倍数的消息。可以表示为L个512位的数据块： Y0,Y1,…,YL-1。其长度为L512 bits。令N=L16,则长度为N个32位的字。令M[0…N-1]表示以字为单位的消息表示。
步骤3：
初始化MD缓冲区。一个128位MD缓冲区用以保存中间和最终散列函数的结果。它可以表示为4个32位的寄存器(A,B,C,D)。寄存器初始化为以下的16进制值。使用低端格式存储。
步骤4：
处理消息块（512位 = 16个32位字）。一个压缩函数是本算法的核心(HMD5)。它包括4轮处理。四轮处理具有相似的结构,但每次使用不同的基本逻辑函数，记为F,G,H,I。每一轮以当前的512位数据块(Yq)和128位缓冲值ABCD作为输入，并修改缓冲值的内容。每次使用64元素表T[1…64]中的四分之一
- T表，由sin 函数构造而成。 T的第i个元素表示为T[i]，其值等于$2^{32}\times abs(sin(i))$,其中i是弧度。由于abs(sin(i))是一个0到1之间的数， T的每一个元素是一个可以表示成32位的整数。T表提供了随机化的32位模板，消除了在输入数据中的任何规律性的特征
步骤5：输出结果。
所有L个512位数据块处理完毕后，最后的结果就是128位消息摘要

消息认证码 MAC

认证码（MAC），也称密码校验和，对选定消息使用一个密钥产生一个短小的定长数据分组，并将它附加在消息中，提供认证功能。
接收方将收到的MAC与计算得出的MAC相比较，若一致则可以判断消息未被更改且来自发送者（前提是只有收发方知道密钥）

消息认证码的用法：

提供认证
提供保密+认证（先认证，再加密）
提供认证+保密（先加密，再认证）

Lec9-10 公钥系统

计算困难性
- 可计算，计算复杂度， P-NP-NPC问题
公钥密码概念
- 单向函数
  - 离散对数
- 单向陷门函数
背包公钥密码
RSA公钥密码
- 参数选取
- 简单的分析
涉及的数论
- 欧拉函数
- Fermat定理
- 素数测试
基于离散对数的密码
- Diffie-Hellman密钥交换
- ElGamal公钥加密算法
椭圆曲线
- 椭圆曲线密码ECDSA
公钥系统的安全问题
- 中间人攻击问题
  计算困难性

计算复杂性

可计算性： 涉及问题是否可以通过算法来解决。
计算复杂度： 衡量解决问题所需的计算资源，通常以时间和空间为度量。

P-NP-NPC问题

P问题： 可在多项式时间内解决的问题。
NP问题： 可在多项式时间内验证给定解的问题。
NPC问题（NP完全问题）： 一旦找到了任何NP问题的多项式时间解法，就能将其应用到所有NP问题。

公钥密码概念

公钥密码系统的要求

每个用户可以方便快捷地产生自己的公私钥对(SK ,PK)
方便快捷地利用公钥PK 对某个消息M 进行加密： $C = E_{P_K}[M]$
如果拥有私钥SK可以方便快捷地对某个密文进行解密：
$M = D_{S_K}[C]$
对于其他人:
- 已知公钥$P_K$ 不能得出私钥$S_K$；
- 已知公钥$P_K$ 和密文$C$，不能得出明文$M$；

单向函数

给定x，计算y=f (x)是容易的；给定y, 计算x使y=f (x)是困难的

离散对数问题： 计算 $a^x \mod p = b$ 中的 $x$。
单向陷门函数
- 容易计算，但难以逆向计算，即给定 $f(x)$ 很容易，但给定 $f(x)$ 求解 $x$ 难。
  背包公钥密码

RSA公钥密码

参数选取

大素数的选择： 关键参数为两个大素数 $p$ 和 $q$，其乘积 $n = pq$ 极难分解。
简单的分析
公钥：$(n, e)$
私钥：$(n, d)$
加密：$c \equiv m^e \mod n$
解密：$m \equiv c^d \mod n$
涉及的数论

欧拉函数

$\phi(n)$ 表示小于等于 $n$ 且与 $n$ 互质的正整数个数。
Fermat定理
如果 $p$ 是素数，那么对于任意 $a$，$a^{p-1} \equiv 1 \mod p$。
素数测试
判断一个数是否为素数的算法，如Miller-Rabin测试。

基于离散对数的密码

Diffie-Hellman密钥协商

允许两个远程方在不共享密钥的情况下协商出一个共享密钥，基于离散对数问题的难解性。

是公钥体制的思想来源，但其本身不是公钥加密算法
是基于公钥的密钥分配算法
- 不可以被用于交换任意消息（不是加密算法）
- 而是用于建立一对密钥
- 仅交互双方知道密钥
密钥的值依赖于双方参与者的公开信息和私有信息
安全性依赖于离散对数问题的困难性

步骤

初始化

用户得到全局参数
- 大素数p
- 模p的原根g
各个用户（如： Alice）生成各自的公私钥对
- 选择私钥：正整数 $x_A< p$
- 计算公钥：$y{A} \equiv g^{x{A}}(\bmod p)$
各个用户公开自己的公钥

密钥交换

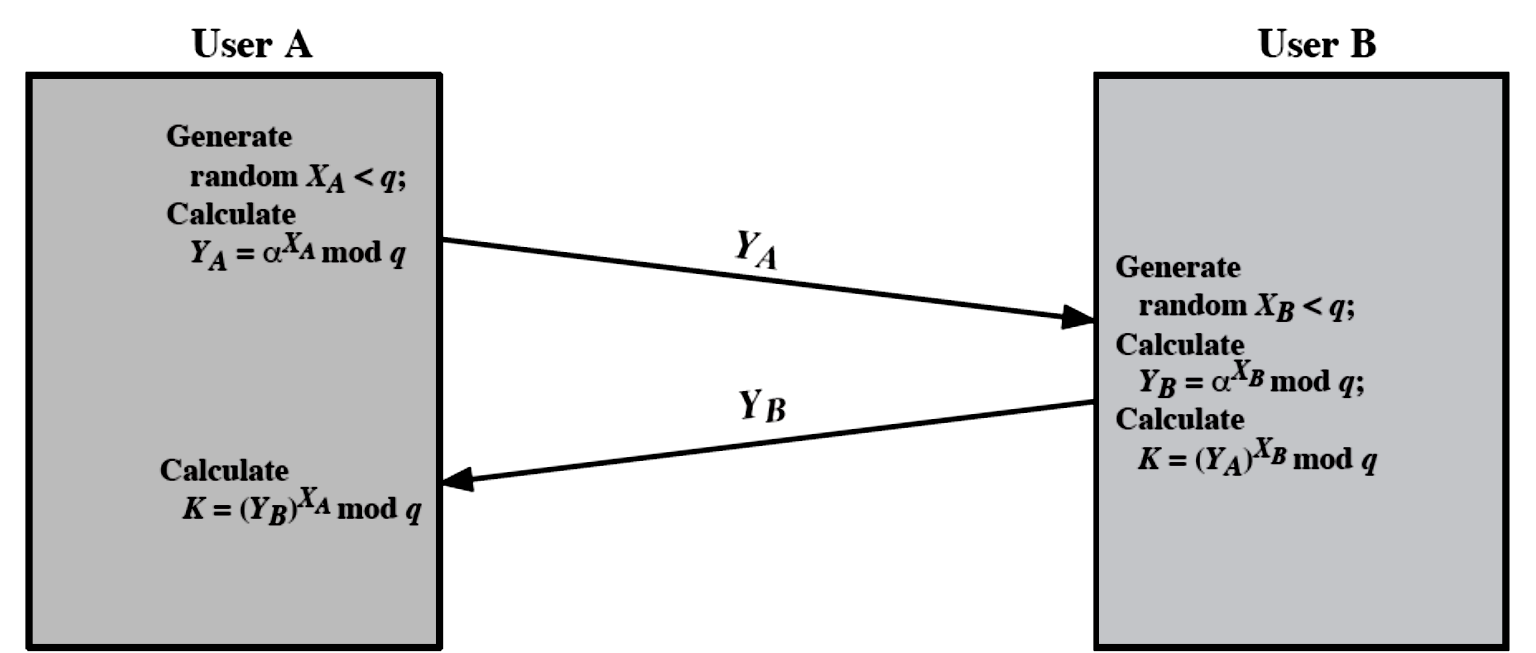
适用于参与者为2个的情形（双方密钥交换），假设参与者为Alice和Bob
Alice用自己的私钥和Bob的公钥计算
Bob用自己的私钥和Alice的公钥计算
则有 $y_{A} \equiv g^{x_{A}}(\bmod p)\begin{array}{l} K \equiv y_{B}^{x_{A}}(\bmod p) \quad K^{\prime} \equiv y_{A}^{x_{B}}(\bmod p) \\ K \equiv y_{B}^{x_{A}} \equiv\left(g^{x_{B}}\right)^{x_{A}} \equiv\left(g^{x_{A}}\right)^{x_{B}} \equiv K^{\prime}(\bmod p) \\ K=K^{\prime} \end{array}$

中间人攻击

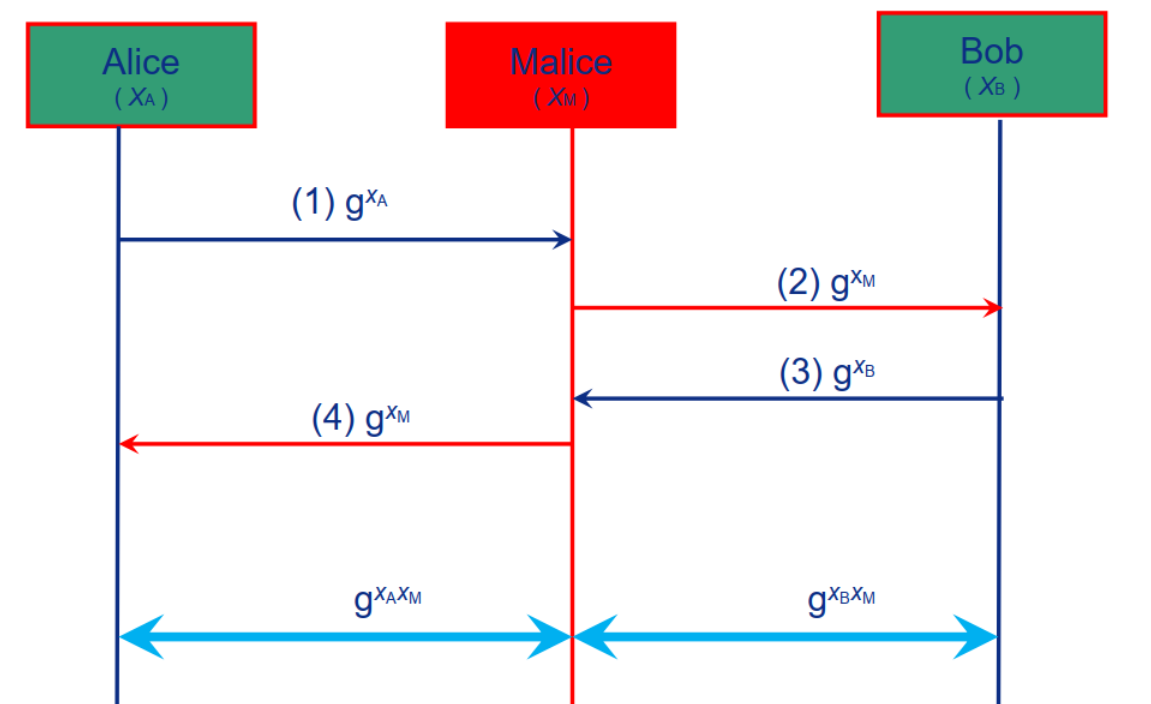
身份与公钥无绑定关系导致的

ElGamal公钥加密算法

概要： 使用离散对数问题作为基础，提供了一种基于公钥的加密系统，适用于安全的密钥交换和加密通信。

椭圆曲线密码

在相同安全程度要求下，所需要的密钥规模要小得多

ECDSA

概要： 使用椭圆曲线上的数学问题，如椭圆曲线上的离散对数问题，作为基础，用于数字签名，提供了与传统RSA等算法相比更高效的加密和签名性能。

SM2

符号约定

KDF()：代表用输入计算出一个给定长度的随机数
H()：代表用输入计算出哈希(散列)函数值
所有指数运算都在椭圆曲线群上进行

具体过程

密钥生成
- 选择私钥$x$, 计算公钥$\mathrm{g}^{x}$
加密算法
- 选择随机数$k$
  - 计算公钥$C_1=g^k$
  - 计算$KDF( ( \mathrm{g} ^{x}) ^{k})$
- 计算$C_{2}=KDF( ( \mathrm{g} ^{x}) ^{k}) \oplus M$
  - 使用KDF算法以公钥$g^x$的k次作为种子计算随机数，与消息异或得到加密值
- 计算$C_{3}= H( C_2, M)$
  - 使用哈希算法作为$C_2|M$的消息认证
- 密文$C{=}C{1}\left|C{2}\right|C_{3}$
  - 将公钥、加密值和消息认证值连接作为密文
解密算法
- 计算 $M= C_2\oplus KDF( (C_1) ^{\mathrm{x}})$
  - 不需要计算随机数k，而是直接利用C_1部分
  - 私钥为x，计算$C_1^x$，作为种子得到其KDF随机数
  - 与第二部分$C_2$异或得到解密消息
- 验证 $C_{3}= H(C_2, M)$ 是否成立
  - 通过哈希算法检验$C_2|M$的消息认证
- 若成立，输出$M$为解密结果；否则报错并退出

正确性检验

$\begin{align} M & = D(E(M)) \\ & = D(C_1,C_2) \\ & = C_2\oplus KDF( (C_1) ^{\mathrm{x}}) \\ & = (KDF( ( \mathrm{g} ^{x}) ^{k}) \oplus M)\oplus KDF( (g^k) ^{\mathrm{x}})\\ & = M \end{align}$

Lec11 数字签名

数字签名及其作用，数字签名的特征（不可伪造）
直接数字签名原理
RSA， DSS， SM2签名方案
公钥的分配途径（特别是公钥证书）
数字签名的安全模型

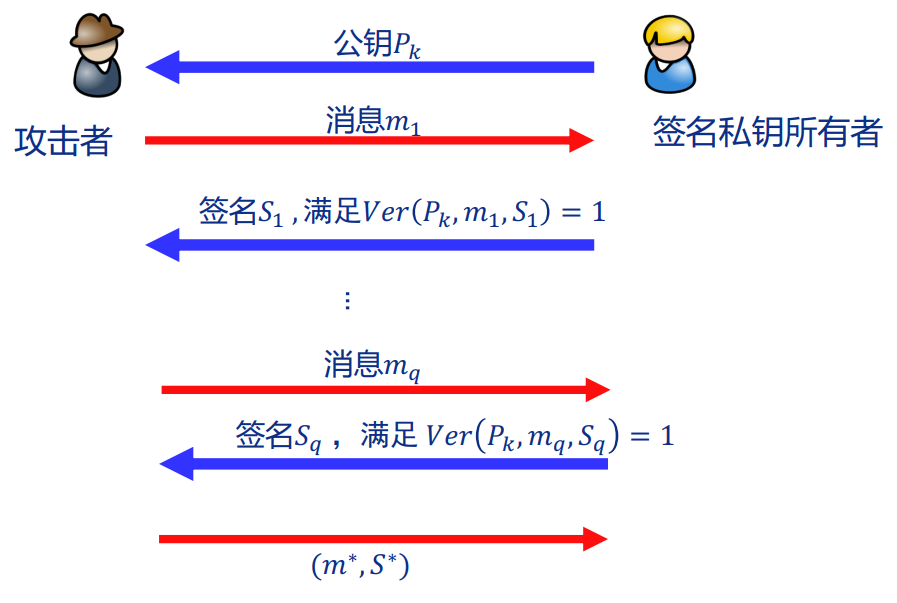
数字签名体制包含下列6个部分：

消息空间$M$：需要签名的所有消息的集合
签名空间$S$：所有可能签名的结果
密钥空间$K$：签名与验证需要的所有可能的私钥/公钥对的集合
密钥生成算法$Gen$
签名算法$Sign$
验证算法$Verify$

RSA签名方案

基础Ver

公钥$pk = (n,e)$，私钥$sk = d$
用$d=sk$ 进行加密获得密文$S=M^d \mod n$
给定$M||S$ 可由 $M = S^e \mod n$ 验证

-> 存在问题

签名的存在性伪造：$M^d \times M^d = M^{2d},M’ = M \times r^e$
长文件 -> 分组签名？（实际上签名的是文件的Hash值）

实用Ver

公钥$pk = (n,e)$，私钥$sk = d$，H为密码学安全的Hash函数
签名过程：
- 需签名的文件M为任意长度
- $M’ = H(M), 0<M’<n$
- 签名 $S=(M’)^d\mod n$
验证过程
- 给定$M||S$ 可由 $H(M) = S^e \mod n$ 验证

PKCS1 签名

H：抗碰撞Hash，长度为$h$，要求$ℎ < 𝑡 - 88$
DI： DigestInfo，是对Hash函数H的编码
FF：填充，使得加上 $H(m)$ 后的长度正好是 $t$ bit
对D用RSA签名

为何要填充至固定长度？

避免 $𝐻(𝑚1) = 𝑝1, 𝐻(𝑚2) = 𝑝_2,且𝐻(𝑚3) = 𝑃{1}𝑃_{2}$ 的ChosenMessage-Attack

DSS签名

H: 哈希函数

p: 素数，其中素数的范围应大于2048bits, 比如2189，二进制写为100010001101，就是12bits。
q: 质数p满足$p|(q-1)$
g: $g = h^{(p-1)/q} \mod p, 1 < h < p-1$
x: 随机生成的私钥, 0 < x < p
y: $y = g^x \mod p$, 公钥为$(p,q,g,y）$

k: 随机选择数, 范围同样是 $0 < k < p$

签名过程
$r = g^k \mod p \mod q$
$s = k^{-1} (H(m) + x r ) \mod q$
$(r,s)$组成数字签名

验证过程
$w = s^{-1} \mod q$
$a = H(M) \times w \mod q, b = r \times w \mod q$
$v = g^{a}y^{b} \mod p\mod q$
通过$v?= r$来验证

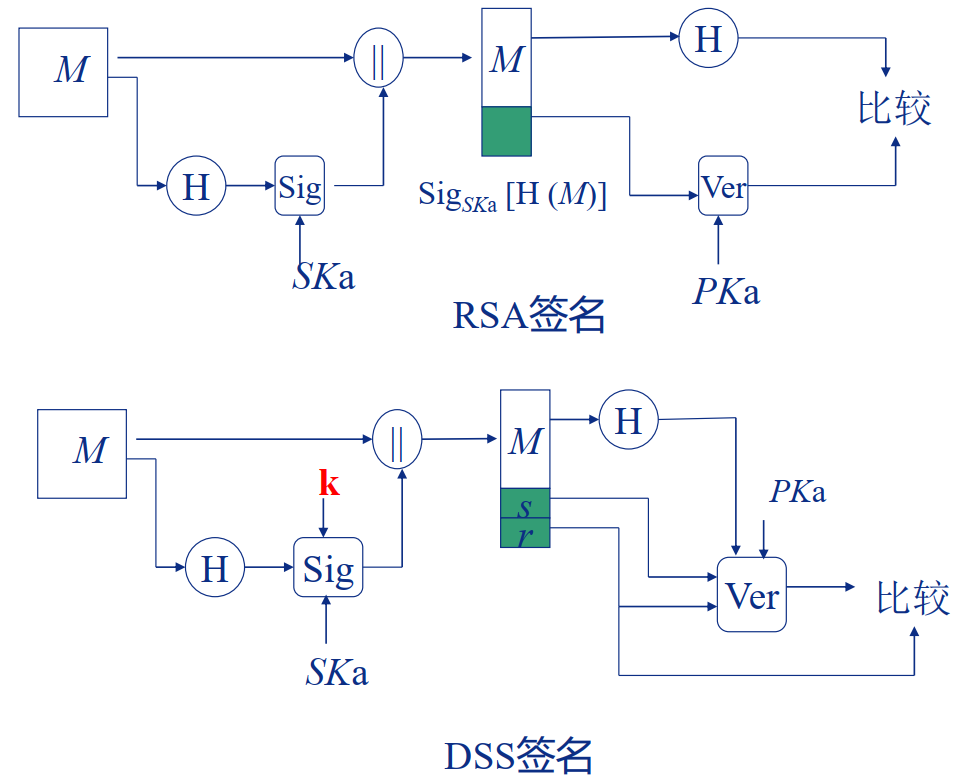
正确性证明

要证$v = r$，只需证明$g^{u_1} \cdot y ^ {u_2} \equiv g^k \pmod p$

$\because g^q \equiv 1 \pmod p$
$\therefore \forall n \in N, g^n \equiv g^{n \bmod q} \pmod p$
$\because y = g^x \bmod p$

$\begin{align*} \therefore g^{a} \cdot y^{b} & = g^{a} \cdot g^{x \cdot b} \pmod p\\ & = g^{a + x \cdot b} \pmod p\\ &= g^{(H(m) + xr) \cdot w \bmod q} \pmod p\\ &= g^{\frac{H(m) + xr}{H(m_0) + xr}\cdot k \bmod q} \pmod p \end{align*}$

$m == m_0 \iff g^{\frac{H(m) + xr}{H(m_0) + xr}\cdot k \bmod q} \bmod p = g^k \bmod p \iff v == r$

即$m == m_0 \iff v == r$ ，验证函数成立。

公钥分配

公钥加密和签名算法的问题

密钥如何管理？
- 公钥的前提：公开自己的密钥
- 难点：不能轻易接受其他人的公钥
- 特点：关键不在于加密，而是认证
Hash函数的安全性？
- 不安全的Hash函数直接导致签名不安全

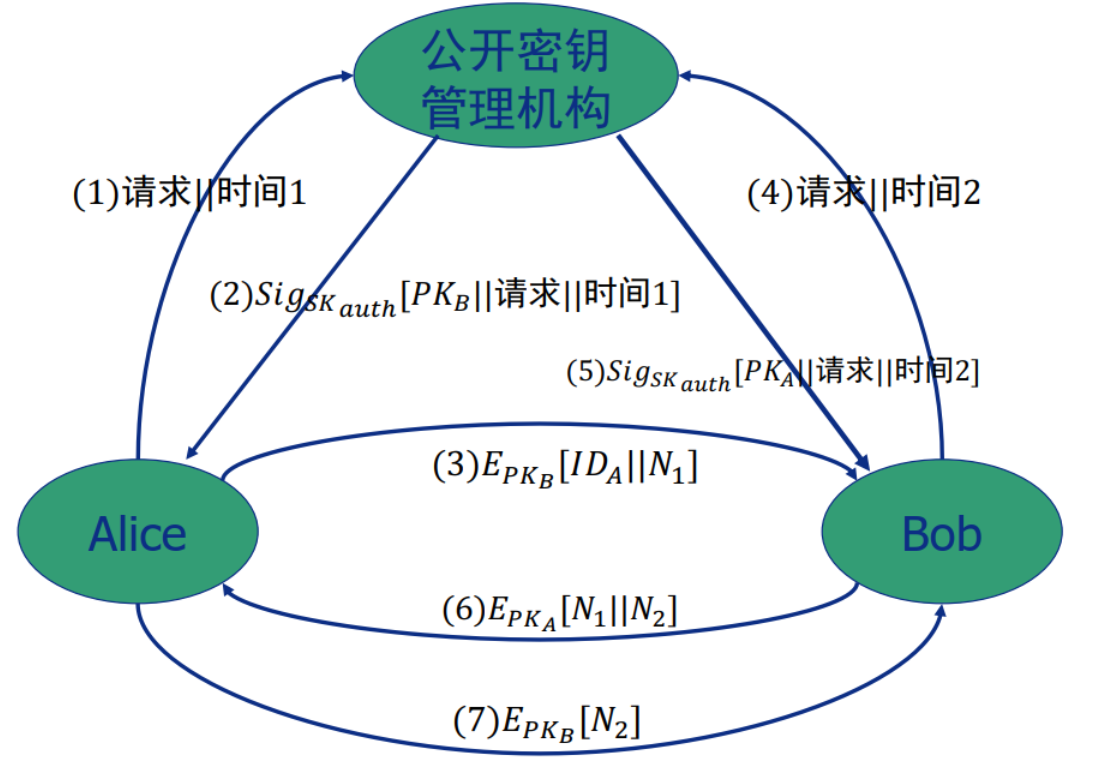
公钥授权

A发送带时间戳的消息给公钥管理员，请求B当前公钥;
管理员用自己的私钥签名一条消息（含B的公钥、 A的请求、原始时间戳）给A， A可确认消息来自管理员;
A保存B的公钥，生成一个挑战（临时交互号）
B用1-2步的方法从公钥管理员处得到A的公钥
对A的挑战形成响应，并对A形成新挑战（N2）
A响应B的挑战

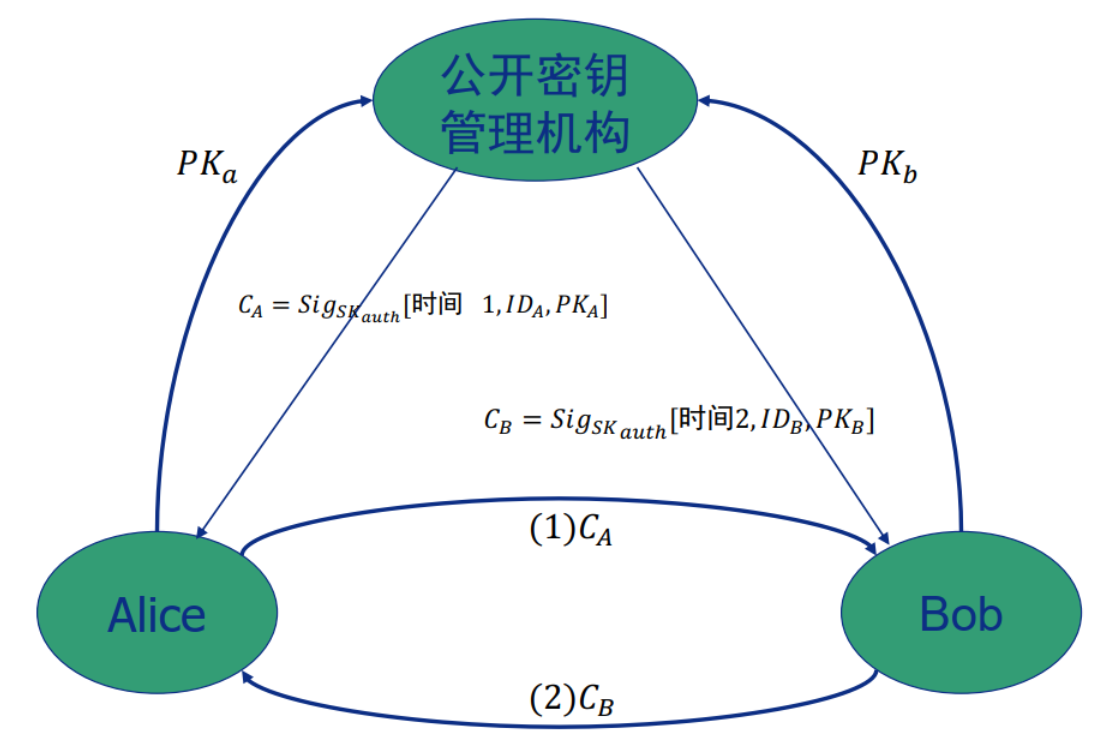
公钥证书

由Kohnfelder提出
思想：通信各方使用证书来交换密钥，而不是通过公钥管理员
安全性与从公钥管理员处获得的密钥的可靠性相同
证书由证书管理员产生
- 包含公钥和其他信息
- 发给拥有相应私钥的通信方
- 通信一方通过传递证书将公钥传给另一方
- 其他人可以验证证书确实是由证书管理员产生的
要求
- 任何人都可以读取证书并确定证书拥有者的姓名和公钥
- 任何人可验证证书是真实的
- 任何人可验证证书是新鲜的（加入时间戳，时间一到更新公钥）
- 只有证书管理员才能产生和更新证书
效果：类似信用卡

Lec12 网络认证服务

Identification， Kerberos与X.509认证服务

Identification

身份认证及可能攻击形式

身份认证协议的成员：证明人 VS. 验证人之间的交互协议
- 证明人Prover：有一个秘密钥（secret key，简写sk）用于向验证人证明自己的身份
- 验证人Verifier：有相应的验证密钥（verification key，简写vk）用于验证证明人的说法
可能的攻击形式
- 直接攻击：攻击者不能窃听，除开公开信息外一无所知（电子门禁）
- 窃听攻击：攻击者可以窃听到证明人和验证人之间的一次或多次交互（无线车钥匙）
- 主动攻击：攻击者利用交互过程来假冒证明人/验证人（ATM，在线银行）

身份认证协议基本组成

密钥生成算法：输出验证密钥vk，秘密钥sk
证明算法：证明人使用sk产生证明
验证算法：验证人使用vk验证证明人的输出。
- 验证通过输出Accept
- 否则输出Reject

基于口令（Password）的身份认证

字典攻击：来源于人类使用的口令往往不是随机的

在线字典攻击
- 在线针对一个ID使用可能的口令进行穷举，可以根据口令可能的概率来提高攻击成功率；也可根据一个高概率口令来穷举ID。对抗方法为阶梯式提高服务器响应时间。
离线字典攻击
- 攻击者攻破login服务器，获得口令数据库，针对ID依据H(pw)尝试计算pw
带预处理的离线字典攻击：
- 攻击者可预先针对全部可能的口令计算出Hash值，再根据收到的验证密钥进行对比

如何提高字典攻击的难度？

加公开盐（public salt）
- sk=pw， vk=H(pw, salt)，扩大字典尺寸
- 提高预处理字典攻击的难度（salt空间应该足够大）
加秘密盐（secret salt）
- sk=pw, vk=(salt, H(pw, salt, pepper))
- pepper很短但不包含在文件中，因此服务器也需要进行一定的穷举，才能完成验证
- 提高离线字典攻击难度，且没有增加用户的记忆难度
使用慢hash函数 H(d)(x)=H(H(H…H(x)))
- 使用者“几乎”无感，离线字典攻击者难度大大提升
- 典型算法是PBKDF2
使用需要高存储代价的hash函数（Memory hard hash)
- 直观上说，算法需要保存很多中间步骤，从而消耗memory，降低并行硬件攻击

一次口令认证

基于一次口令（One time Password）的身份认证（抵御窃听攻击）
- 窃听攻击模型：攻击者可以窃听到证明人和验证人之间的交互。并试图利用
  窃听的结果来假冒证明人
- 在窃听攻击下，原始基于口令的身份认证无效
一次口令：每次协议运行后，口令均更新
一个简单的例子：
- 证明人和验证人有同样的k，证明人每次用k加密一个验证人知道的counter值给验证人（随后counter自加1），加密的结果看作一次口令.
需要同步：使用时间窗

挑战响应协议

主动攻击模型：攻击者先模拟成验证人，并与拥有sk的证明人交互（并发或者顺序）；再利用交互的结果，试图向真正的验证人（拥有vk）假冒成合法证明人。
主动攻击下，一次口令认证失效
实现方式
- 利用消息认证码： vk = s k= MAC Key；验证人随机选择挑战m，证明人发
  出的响应信息是密钥和挑战的一个Mac值
- 利用签名：实现非秘密vk的挑战响应身份认证

Kerberos

X.509

X.509 是关于证书结构和认证协议的一种重要标准，并被广泛使用。
X.509 是基于公钥密码体制和数字签名的服务。
版本(Version)：区分合法证书的不同版本，默认设置为1。如果存在发行商唯一标识或主体唯一标识，则版本号为2；如果存在一个或多个扩展，则版本号为3。
序列号(Serial number)：一个整数，在CA中唯一标识证书。
签名算法标识(Signature algorithm identifier)：带参数的、用于给证书签名的算法，由于此信息在证书尾部的域Signature中还会出现，这里很少含该信息。
发行商名字(Issue name)： X.509中创建、签名证书的认证中心CA的名字。
有效期(Period of validity)：包含两个日期，即证书的生效日期和终止日期。
证书主体名(Subject name): 获得证书的用户名，证明拥有相应私钥的主体是公钥的所有者。

Lec13 IP/Web安全

❖应用层： SET/SHTTP
❖传输层： SSL/TLS
❖网络层： IPSec

❖了解安全Web安全的需求
❖了解SSL协议的基本构成，并熟悉

SSL握手协议
❖了解有SSL协议的应用
自己动手使用配置有关SSL的应用
❖熟悉
IPSec security framework
AH, ESP
key management & Oakley/ISAKMP
❖了解有哪些IPSec应用的低端产品
自己尝试去使用、配置

SSL概况

协议分为两层
- 上层： SSL握手协议、 SSL修改密文协议、 SSL告警协议
- 底层： SSL记录协议
SSL记录协议
- 建立在可靠的传输协议(如TCP)之上
- 它提供连接安全性，有两个特点
  - 保密性，使用了对称加密算法
  - 完整性，使用HMAC算法
用来封装高层的协议

SSL握手协议
- 客户和服务器之间相互认证
- 协商加密算法和密钥
- 它提供连接安全性，有三个特点
  - 身份认证，至少对一方实现认证，也可以是双向认证
  - 协商得到的共享密钥是安全的，中间人不能够知道
  - 协商过程是可靠
SSL不强制要求双向的认证

SSL过程

SSL（Secure Sockets Layer）的三次握手是建立安全连接的过程，用于确保通信的机密性和完整性。SSL已经被其后继标准TLS（Transport Layer Security）所取代，但两者的三次握手过程基本相同。

以下是SSL/TLS的三次握手过程：

客户端Hello（ClientHello）：
- 客户端向服务器发送一个ClientHello消息，其中包含以下信息：
  - 支持的SSL/TLS协议版本。
  - 一个随机数，用于生成后续的密钥。
  - 支持的加密算法和压缩方法。
服务器Hello（ServerHello）：
- 服务器选择一个与客户端支持的协议版本、加密算法和压缩方法相匹配的配置，并向客户端发送一个ServerHello消息，其中包含以下信息：
  - 选定的SSL/TLS协议版本。
  - 一个随机数，用于生成后续的密钥。
  - 服务器选择的加密算法和压缩方法。
服务器证书（Server Certificate）和密钥交换消息：
- 服务器发送包含数字证书的Server Certificate消息，证书中包含服务器的公钥。该证书由数字签名机构（CA）签发，用于验证服务器身份。
- 如果服务器要求客户端提供证书，服务器还可以发送一个CertificateRequest消息。
- 服务器发送一个ServerKeyExchange消息，用于密钥协商，具体内容取决于使用的密钥交换方法。
完成服务器Hello（ServerHelloDone）：
- 服务器发送一个ServerHelloDone消息，表示握手消息的结束。
客户端证书和密钥交换消息（可选）：
- 如果服务器要求客户端提供证书，客户端会发送一个包含数字证书的ClientCertificate消息。
- 客户端还可能发送一个ClientKeyExchange消息，包含用于密钥协商的信息。
握手完成（Finished）：
- 客户端和服务器分别计算握手消息的hash值，使用之前交换的随机数和密钥，然后将这个hash值发送给对方。
- 一旦接收到对方的握手消息hash值，双方可以验证握手的完整性，确认安全连接已建立。
- 握手完成后，SSL/TLS连接就建立完成，可以进行加密的通信了。

这个三次握手过程确保了通信的安全性，防止中间人攻击，同时协商双方能够支持的加密算法和其他参数。在握手完成后，客户端和服务器将共享密钥，用于保障后续通信的机密性。

Lec14 安全邮件

电子邮件的主要协议

Mail User Agent (MUA)
- 接受用户输入的指令，将邮件传送至信件传输代理
- 或通过pop/imap将信件从传输代理服务器取到本机上
- 常见的有foxmail， outlook express等邮件客户程序
Mail Transfer Agent (MTA)
- 翻译邮件地址并选择最传佳路径转发邮件, 激活传输代理程序
Simple Mail Transfer Protocol (SMTP):
- 基于TCP的端到端协议, 邮件从客户机<—>服务器， (RFC 821)
POP和IMAP：通称为消息存储MS
- Post Office Protocol,用户的MTA和服务器通讯并下载邮件
- Internet Message Access Protocol,在Client端管理Server上的邮箱
Mail Delivery Agent (MDA)
- 邮件投递代理，把邮件放到用户的邮箱（MS）里
- 例如： Sendmail本身并不处理邮件投递，由邮件投递代理或邮差来投递包括UUCP投递代理、 TCP投递代理、本地投递代理

PGP

身份认证

发送方
- 产生消息M
- 用SHA-1对M生成一个160位的散列码H
- 用发送者的私钥对H签名，并与M连接
接收方
- 用发送者的公钥验证并恢复散列码H
- 对消息M生成一个新的散列码，与H比较。如果一致，则消息M被鉴别。

保密

发送方
- 生成消息M并为该消息生成一个随机数作为会话密钥
- 用会话密钥加密M
- 用接收者的公钥加密会话密钥并与消息M结合
接收方
- 用自己的私钥解密恢复会话密钥
- 用会话密钥解密恢复消息M
PGP采用CAST-128(或IDEA或3DES)、 64位CFB方式。一次性密钥，单向分发，公钥算法保护。
- 公开密钥算法的长度决定安全性RSA(768~3072)、 DSS(1024)

两种服务都需要时，

发送者先用自己的私钥签名，
然后用会话密钥加密，再用接收者的公钥加密会话密钥。
一个用户有多个公钥/私钥对时，接收者如何知道发送者是用了哪个公钥来加密会话密钥？
- 将公钥与消息一起传送。
- 将一个标识符与一个公钥关联。对一个用户来说做到一一对应。
- 定义KeyID 包括64个有效位： (KUa mod 2^64)
- KeyID同样也需要PGP数字签名。

信任关系

尽管PGP没有包含任何建立认证权威机构或建立信任体系的规格说明，但它提供了一个利用信任关系的手段，将信任与公钥关联，利用信任信息。

Key legitimacy field：表明PGP将信任这是一个对该用户是合法的公钥；信任级别越高，这个userID对这个密钥的绑定越强。这个字段是由PGP计算的。
每一个签名与一个signature trust field关联，表明这个PGP用户对签名人对公钥签名的信任程度。 Key legitimacy field 是由多个signature trust field 导出的。
Owner trust field：表明该公钥被信任用于签名其它公钥证书的信任程度。这一级别的信任是由用户给出的。

S/MIME

S/MIME更象商用或组织使用的工业标准，而PGP更面向个体用户选用。

密码学与信息安全基础-CS3314

Lec1 序论-计算机安全概况

安全定义

安全防护

安全服务 安全策略与安全机制

安全模型

Lec2 古典加密技术

密码学基本概念

古典密码技术

基于代换技术的古典密码体制

Caesar

单表代换密码

多表代换密码

Playfair

Hill

Vigenère Cipher

一次一密 OneTimePad

基于置换技术的古典密码体制

乘积密码

隐写术

结论

Lec3-4 常用密码算法

对称加密

流密码

分组密码

SPN密码

初步做法：CDP

进一步的做法：SPN

Feistel密码

DES算法

IDEA

AES

SM4

Lec5 分组码应用模式与伪随机数

ECB (Electronic CodeBook)

CBC (Cipher Block Chaining)

CFB (Cipher FeedBack)*

OFB (Output FeedBack)

CTR (Counter)

分组码应用模式小结

随机数

伪随机数产生器 (C++ 的RND)

用分组密码产生的随机数

BBS产生器 (Blum整数)

Lec6 保密通信

Lec7 消息认证和Hash函数（认证性）

消息认证和认证函数

三类产生认证符的函数

报文加密

对称加密

公钥加密

散列函数

散列函数的算法

MD5算法

消息认证码 MAC

Lec9-10 公钥系统

计算困难性

计算复杂性

P-NP-NPC问题

公钥密码概念

公钥密码系统的要求

单向函数

背包公钥密码

RSA公钥密码

参数选取

简单的分析

涉及的数论

欧拉函数

Fermat定理

素数测试

基于离散对数的密码

Diffie-Hellman密钥协商

步骤

中间人攻击

ElGamal公钥加密算法

椭圆曲线密码

ECDSA

SM2

符号约定

具体过程

安全服务安全策略与安全机制